二、填空题(本大题共15小题，每小题2分，共30分)
请在每小题的空格中填上正确答案。错填、不填均无分。
11.设A，B为两个随机事件，若A发生必然导致B发生，且P（A）=0.6，则P（AB）=_____.
12．设随机事件A与B相互独立，且P（A）=0.7,P(A-B)=0.3,则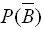
=_______.
13.已知10件产品中有2件次品，从该产品中任意取3件，则恰好取到一件次品的概率等于______.
14.已知某地区的人群吸烟的概率是0.2，不吸烟的概率是0.8,若吸烟使人患某种疾病的概率为0.008，不吸烟使人患该种疾病的概率是0.001，则该人群患这种疾病的概率等于______.
15．设连续型随机变量X的概率密度为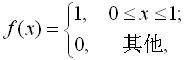
则当
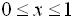时，X的分布函数F(x)=______.
16．设随机变量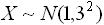
，则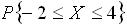
=______.（附：
）
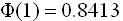17．设二维随机变量（X，Y）的分布律为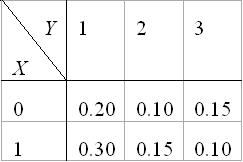
则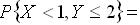
______.
18．设随机变量X的期望E(X)=2，方差D(X)=4，随机变量Y的期望E(Y)=4，方差D(Y)=9，又E(XY)=10，则X，Y的相关系数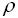
=______.
19．设随机变量X服从二项分布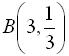
，则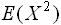
=______.
20．设随机变量X~B（100，0.5），应用中心极限定理可算得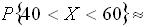
______.
（附：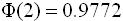
）
21．设总体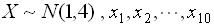
为来自该总体的样本，
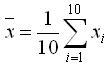,则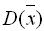
______.
22．设总体,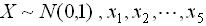
为来自该总体的样本，则
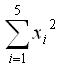服从自由度为______的
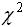分布.
23.设总体X服从均匀分布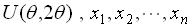
,是来自该总体的样本,则
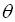的矩估计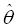
=______.
24.设样本
来自总体
,假设检验问题为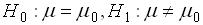
,则检验统计量为______.
25.对假设检验问题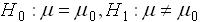
,若给定显著水平0.05,则该检验犯第一类错误的概率为______.
三、计算题(本大题共2小题，每小题8分，共16分)
26.设随机变量X与Y相互独立,且X~N(0.1),Y~N(1,4).
(1)求二维随机变量(X,Y)的概率密度f(x,y);
(2)设(X,Y)的分布函数为F(x,y),求F(0,1).
27.设一批产品中有95%的合格品,且在合格品中一等品的占有率为60%.
求:(1)从该批产品中任取1件,其为一等品的概率;
(2)在取出的1件产品不是一等品的条件下,其为不合格品的概率.
四、综合题(本大题共2小题，每小题12分，共24分)
28.设随机变量X的概率密度为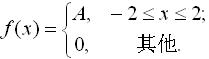
试求:(1)常数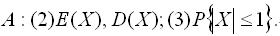
.
29.设某型号电视机的使用寿命X服从参数为1的指数分布(单位:万小时).
求:(1)该型号电视机的使用寿命超过t(t>0)的概率;
(2)该型号电视机的平均使用寿命.
五、应用题(10分)
30.设某批建筑材料的抗弯强度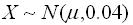
,现从中抽取容量为16的样本,测得样本均值
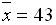,求μ的置信度为0.95的置信区间.(附:
)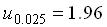